2014.08.06
Squall line เป็นแนวฝนแบบ Convective
ที่จัดเรียงตัวกันในมาตราส่วน Meso scale คิดง่ายคือ
ประมาณหลักร้อยกิโลเมตรนั่นคือ
พื้นที่เรดาร์ตรวจอากาศภาคพื้นดินสามารถตรวจจับรูปแบบการเคลื่อนที่ของฝนนี้ได้
ในแถบอินโดจีนมีโปรเฟสเซอร์ Prof.Takehiko Satomura ได้ทำการอธิบายและเสนอกลไกการกำเนิดรูปแบบฝนชนิดไว้แล้ว
ในปี2000 น่าเสียดายที่ท่านได้จากโลกนี้ไปแล้วเมื่อเดือนมีนาคม 2014 ท่านเป็นอาจารย์ของผมเอง
หากแต่ไอเดียท่านยังอยู่กับพวกเรา
แนวคิดภาพตัดขวางแนวดิ่ง RHI
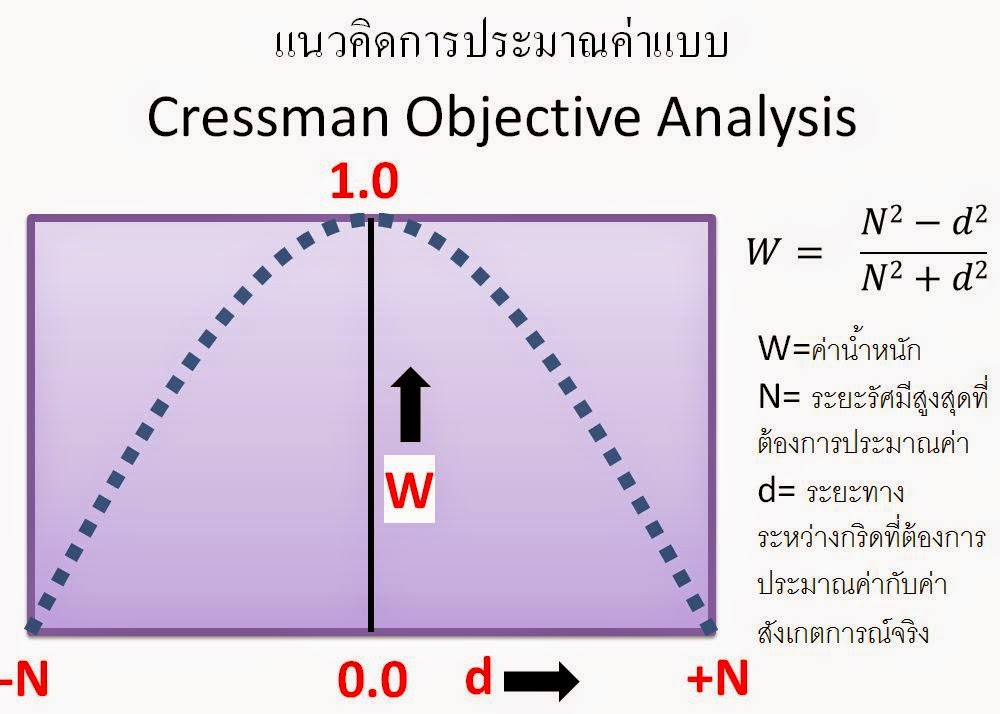
ผมได้ทดลองทำการนำการประมาณค่าแบบ
Inverse
Distance Weighted IDW มาใช้กับข้อมูลเรดาห์ที่ตรวจอากาศแบบหลายมุม (เหมือนจะง่ายแต่ใช้เวลาพอควรเลยครับ ตอนใช้พวกGIS เนี่ยแค่คลิกไม่กี่ที 555 )ข้อมูลนำเข้าได้จากการ extract ข้อมูลเรดาร์ด้วย Library แล้วเก็บในรูปของไบนารี่ที่เป็นฟอร์แมทของผมเอง
ผมใช้ข้อมูลไบนารี่ตัวนี้ในการทดลองทำภาพที่ชื่อว่า Range-Height-Indicator (RHI) เป็นภาพแนวดิ่งของเรดาร์ขณะที่ Squall กำลังเคลื่อนตัวผ่านที่ตั้งของเรดาร์ โดยผมเขียนโปรแกรมเลือกข้อมูลหนึ่งมุมอซิมุธ
หลายมุมยก แต่ละมุมยกจะมีความละเอียดที่เราเรียกว่า Bin size โดยภาพที่ได้ข้างล่างเป็นการประมาณค่า dBZ ของฝนแบบ Squall ในตอนเย็น
โปรแกรมยังมี Bug อยู่
ต้องแก้นิดหน่อยเลยโพสบางส่วนให้เป็นไอเดียครับ ขั้นตอนในโปรแกรมFortran คือ
1.
อ่านเรดาร์แบบ Volume ไฟล์ และเลือกมุมอซิมุทที่ต้องการ Plot เลือกความสูง
ระยะทางของเรดาร์บีม
2.
คำนวนความสูงและระยะทาง ของแต่ละจุดที่เรดาห์ได้ทำการบันทึกข้อมูล
3.
เรียกซับโปรแกรมเพื่อประมาณค่าจุดเรดาร์ในแต่ละมุมยก ด้วย IDW
ตัวอย่างฝนชนิด Squalline
program
create_RHI
!-------------------------------------------------------------
! 2014.08.06 NATAPON MAHAVIK
! to create data for plotting Range-Height-Indicator [RHI]
! from extracted radar of
Phetchabun by Gematronik library
! data stor at
/home/mnattapon/RAID3storage4/research_icp/
!
analysis_phb_alg/radar_ans/cal_RHI_PPI_CAPPI_rad/cal_RHI
! data of selected azimuth will be
interpolate by IDW
!-------------------------------------------------------------
implicit none
integer,parameter ::
sizeofreal=4 !-record size
integer :: i,j,m,n
real, parameter :: pi =
4*atan(1.0) !- exploit intrinsic
atan to generate pi
real,parameter ::
d2r=pi/180.0 !- radian
conversion degree to radian
real,parameter :: k2m=1000.0 !- km to meters
real,parameter :: NA=-9999.0 !- no radar data
!-radar variables
integer :: rn !-record number
integer :: maxelv !-max number of
elevations
real :: elv_rad ! elevation
angle in radian
character*10 :: path
real :: rgate ! real(igate) = gate "km"
real :: rbin ! real(irbin) = rbin "km"
integer :: ielv, iazm, ibin
integer :: maxazmt !-Max number of
rays as temp var
integer:: maxbin ! Max number of
range
integer,parameter ::
maxazmf=1000 !-Max number of
rays as my asssumption!!!
real, dimension(:,:,:), allocatable
:: rdata !-Radar data
real, dimension(:,:),
allocatable :: elv !-Elevation angles
real, dimension(:,:),
allocatable :: azmth !-Angles [ in mathematic in degree]
real,dimension(:,:), allocatable
:: azmth_rad !-Angles [in azimuth in
radian]
integer,dimension(:),allocatable
:: maxazm !-Max number of rays
depending on sweeps
real,dimension(:,:,:),allocatable
::beam_dist_hz !-beam distance in
horizontal plain in m.
real,dimension(:,:,:),allocatable
::beam_height !-beam height by reinhart
p62 in m.
integer,parameter::re=6374000. !-earth radius in m.
real,parameter ::rr=4./3.*re !-reinhart p62 as R' in
m.
real,parameter :: rad_alt=97. !-radar altitude above MSL
from calculation DEM.(GG~73)
real :: h_rd=30. !-height of
radar antenna by estimate TMD using 30m
integer :: az_int !-round up real azimuth to interger [degree]
real,parameter :: sel_az=225.0 !-selected azimuth degree
real,parameter ::
min_dbz=10.0,max_dbz=100.0 !-max and
min dbz
real,parameter :: max_dist=200.0 !-max distance for RHI in km
real,parameter :: max_high=15.0 !-max hight for RHI in km
!-output var for interpolation
real, dimension(:,:), allocatable
:: dbz !-dbz at elevation(i) & bin number(i) [dBZ]
real, dimension(:,:), allocatable
:: height !-height from ellipsoid
at elevation(i) & bin number(i) [km]
real, dimension(:,:), allocatable
:: dist_x !-distance from radar
site at elevation(i) & bin number(i)[km]
real, parameter :: res=1.0 !- unit in km
integer,parameter :: nx=max_dist/res !- number of x pixels
integer,parameter ::
ny=max_high/res !- number of
y pixels
real, dimension(nx,ny)::
outp_intp !- interpolated
output
real, parameter :: radi=2.0 !-radius of interpolation
in idw [km]
!-read radar binary
!-cut
rn=1
open(10,file=trim(path)//'PHB1008102100.dat',form='unformatted',access='direct',recl=sizeofreal)
read(10,rec=rn) maxelv
!-cut
!-initialize output
dbz=NA;height=NA;dist_x=NA
do ielv = 1, maxelv
maxazmt=maxazm(ielv)
do
iazm = 1, maxazmt
read(10,rec=rn) azmth(iazm,ielv)
rn = rn + 1
!--- convert azmuth to be mathematic angle
!-cut
read(10,rec=rn) elv(iazm,ielv)
rn = rn + 1
do ibin = 1, maxbin
read(10,rec=rn) rdata(ibin,iazm,ielv)
rn = rn + 1
!-cal beam position in horizontal plain
!-cut
!-cal beam height + rad altitude in meter.
!-cut
endif
end do
end do
end do
close(10)
!-call sub IDW interpolate_idw(dbz(height,dist))
print*,'interpolate dbz to idw of
range-height radar ...'
call interpolate_idw(dbz,height,dist_x,maxelv,maxbin,res,nx,ny,radi,max_dbz,outp_intp)
print*,'infos for GRADS ;)
xdef:',nx,'ydef: ',ny,'resolution: ',res
!-write interpolated radar RHI to binary for checking in grads
open
(20,file='rs_interpolated_RHI_radar.bin',form='unformatted',access='direct',
recl=nx*ny*sizeofreal)
write(20,rec=1)outp_intp
close(20)
open
(30,file='rs_interpolated_RHI_radar_ncl.bin',form='unformatted')
write(30)outp_intp
close(30)
deallocate(beam_dist_hz,beam_height);deallocate(rdata,elv,azmth,azmth_rad)
deallocate(maxazm);deallocate(dbz,height,dist_x)
end
program create_RHI
Subroutine
interpolate_idw(dbz,height,dist_x,maxelv,maxbin,res,nx,ny,radi,max_dbz,outp_intp)
implicit none
!-external
integer,intent(in) ::
maxelv,maxbin
real,dimension(maxelv,maxbin),intent(in)
:: dbz,height,dist_x
real,intent(in) :: max_dbz
real,intent(in) :: res !-defined resolution of output grid
[km]
integer :: nx,ny
real,dimension(nx,ny),intent(out)
:: outp_intp
real :: radi !-defined radius for interpolation [km]
!-internal variables
real :: dist !-distance between output grid
and input grid
integer :: sx,ex,sy,ey !-start and end grid of considering box
respected to radius
integer :: i,j,m,n
real,parameter :: NA=-9999.0 !-not
available data
real,parameter :: p=-2 !-power for idw
integer :: x,y !-coordinate of output grid in
input data grid
real :: inv_d !-inverse distance
real :: nw !-normalized weight
real,dimension(nx,ny) ::
sum_invd !-sum inverse distance
real,dimension(nx,ny) ::
sum_nw !-sum normalized weight
!-loop elvation and bin of input data to be fast calculate
!outp_intp=NA
!-1st loop for find summation of inverse distance in output grid
do i=1,maxelv
do j=1,maxbin
if (dbz(i,j)==NA)cycle
!-find box of considering interpolation respected to defined radius
sx=((int(dist_x(i,j))-radi)/res)-res; ex=((int(dist_x(i,j))+radi)/res)+res
sy=((int(height(i,j))-radi)/res)-res; ey=((int(height(i,j))+radi)/res)+res
!-here to avoid error outbound otherwise
segmentation fault
if (sx<=0) sx=1; if (ex>nx) ex=nx; if (sy<=0) sy=1; if (ey>ny) ey=ny
!-loop inside box for calculate summation of inverse distance
do m=sx,ex
do n=sy,ey
!-convert coordinate considering
grid to be same input coordinates
x=(m*res)-res+1; y=(n*res)-res+1
!-calculate euclidean distance
dist=sqrt(abs(x-dist_x(i,j))+abs(y-height(i,j)))
!print*,x,y,dist
!-cal inverse distance and sum all
inverse distance
inv_d=dist**p
sum_invd(m,n)=sum_invd(m,n)+inv_d
enddo
enddo
enddo
enddo
!-2nd loop apply normalized weight to dbz and sum all results of each
ouput grid
do i=1,maxelv
do j=1,maxbin
if (dbz(i,j)==NA)cycle
!-find box of considering interpolation
respected to defined radius
sx=((int(dist_x(i,j))-radi)/res)-res; ex=((int(dist_x(i,j))+radi)/res)+res
sy=((int(height(i,j))-radi)/res)-res; ey=((int(height(i,j))+radi)/res)+res
!-here to avoid error outbound otherwise segmentation fault
if (sx<=0) sx=1; if (ex>nx) ex=nx; if (sy<=0) sy=1; if (ey>ny) ey=ny
!-loop inside box for calculate weight, then apply it
do m=sx,ex
do n=sy,ey
!-convert coordinate considering grid to be same input
coordinates
x=(m*res)-res+1; y=(n*res)-res+1
!-calculate euclidean distance
dist=sqrt(abs(x-dist_x(i,j))+abs(y-height(i,j)))
!-cal inverse distance, normalize and sum all weighted
dbz
inv_d=dist**p
nw=inv_d/sum_invd(m,n)
sum_nw(m,n)=sum_nw(m,n)+nw !-it must be 1.0 in every
grid
outp_intp(m,n)=outp_intp(m,n)+(nw*dbz(i,j))
enddo
enddo
enddo
enddo
!-replace values for grads or NCL plot
where (outp_intp>max_dbz)
outp_intp=0
endwhere
End subroutine interpolate_idw
5.
ตัวอย่างโค้ดของ NCL .ในการ Plot ภาพ RHI โปรแกรมนี้มีอะไรน่าตื่นเต้นเยอะนะครับ
ช่วยในงานวิจัยได้ไม่น้อยเลยครับ
;**********************************************************************
; color_1.ncl
; NATTAPON MAHAVIK
; Concepts illustrated:
;
- Drawing color filled contours using the default color map
; how to read and write data from
f90 to ncl
;
https://www.ncl.ucar.edu/Document/Functions/Built-in/fbinread.shtml
;
;**********************************************************************
load
"$NCARG_ROOT/lib/ncarg/nclscripts/csm/gsn_code.ncl"
load
"$NCARG_ROOT/lib/ncarg/nclscripts/csm/gsn_csm.ncl"
;************************************************
begin
;************************************************
; read in binary
;************************************************
fili="rs_interpolated_RHI_radar_ncl.bin"
recl=200*15
;rad =
fbindirread("rs_interpolated_RHI_radar_ncl.bin",rec,(/15,200/),"float")
r=fbinread (fili, recl , "float")
rad=onedtond(r,(/15,200/))
rad@_FillValue = -9999 ;missing values
;************************************************
; create plot
;************************************************
wks = gsn_open_wks("ps","ps_RHI_radar_PHB") ; open a ps file
gsn_define_colormap(wks,"prcp_1") ; choose color map
res =
True ; plot mods desired
res@vpWidthF = 0.8 ; set width and height
res@vpHeightF = 0.5
res@cnFillOn =
True ; turn on color fill
res@gsnMaximize = True
res@gsnDraw =
False ; don't draw
yet
res@gsnFrame =
False ; don't
advance frame yet
res@cnInfoLabelOn =
False ; not show infomation height
res@cnLineLabelsOn =
False ; not show label
of contour line
res@cnConstFLabelOn = False
res@cnLineThicknessF = 0 ; change line thickness
res@cnLinesOn = False
res@tiMainString =
"Range Height Indicator of Squallline in Thailand"
res@tiXAxisString =
"Distance [km]"
res@tiYAxisString =
"Height[km]"
res@cnLevelSelectionMode = "ManualLevels" ; manually set the contour levels with
the following 3 resources
res@cnMinLevelValF = 10.0 ; set the minimum contour
level
res@cnMaxLevelValF = 60.0 ; set the maximum contour
level
res@cnLevelSpacingF = 5.0 ; contour interval
res@lbOrientation = "vertical" ; vertical label bar
res@lbLabelStride = 2.0
res@gsnSpreadColors=True
plot = gsn_csm_contour(wks,rad,res)
draw(plot) ; note
we are drawing the first one!
frame(wks)
end
สิ่งที่ต้องทำต่อไปคือ แก้โปรแกรมให้ยืดหยุ่น ใช้กับข้อมูลหลายช่วงเวลา นำวิธีการประมาณค่าแบบอื่นๆมาใช้